Software Foundation
Functional Programming
In functional programming, a procedure is considered functional if it has no side effects and its inputs map to outputs. It’s a concerete method for computing a mathematical function.
Functions are first-class values: Functions can be passed to other functions as arguments, returned from functions or included in data structures.
Other features of functional programming include algebraic data types, pattern matching and polymorphic type systems. All these are supported by Coq.
Tags:
Source:
Software Foundation
Enumerated Type Definition
The following defines the type day with members monday, tuesday, etc.

Having defined the type, we can now write functions that operate on it:

The return type day can be inferred instead of being explicitly specified.
The individual elemens (monday, tuesday, etc.) are called constructors
Tags:
Source:
Software Foundation
Compute
Use the Compute command to evaluate a compound expression:

Tags:
Source:
Software Foundation
Example + Proof
Examples serve as assertions using example input and output values to verify expectted behavior of an expression.
Examples can be named so that they can be referenced later.
We can ask Coq to verify the assertion like this:
Tags:
Source:
Software Foundation
If..then..else
If..then..else conditional expressions are support for any inductively defined type with exactly two clauses in its definition.

Tags:
Source:
Software Foundation
Admitted
Admitted can be used as a placeholder for an incomplete proof. Without it, the following example would throw an error.

Tags:
Source:
Software Foundation
Type Checking
Expressions’ return types can be checked using the Check command like so:

Tags:
Source:
Software Foundation
Type Checking of Functions
Types of functions’ clauses and return values can be checked using the Check command with the => syntax like so:

This checks that the function takes bool type and returns a bool type.
Tags:
Source:
Software Foundation
Constructor Arguments
Enumerated types can have constructors that take arguments:

Constructor expressions are formed by applying a constructor to zero or more other constructors or constructor expressions, obeying the declared number and types of the constructor arguments. E.g.,
- red
- true
- primary red
- etc.
But not
- red primary
- true red
- primary (primary red)
- etc.
If p is a constructor expression belonging to the set rgb, then primary p (pronounced “the constructor primary applied to the argument p”) is a constructor expression belonging to the set color.
We can define functions on colors using pattern matching:

Since the primary constructor takes an argument, a pattern matching primary should include either a variable (as above – note that we can choose its name freely) or a constant of appropriate type (as below).

A proof involving a constructor expression looks like this:

Tags:
Source:
Software Foundation
Modules
Modules can be used to limit the scope of definition:

Tags:
Source:
Software Foundation
Tuples
A single constructor with multiple parameters defines a tuple. This is a tuple with 4 values of type bit is defined and checked:

Tags:
Source:
Software Foundation
Tuple Matching
This is how variable of type tuple is created and matched for:

Tags:
Source:
Software Foundation
Definition of Unary Number
Unary (as opposed to binary or decimal) numbers are defined as:

0 is represented by 0, 1 by S 0, 2 by S (S 0) and so on.
The S stands for “successor”.
0 and S are arbitrary; they define a representation of numbers. Other marks could have been used instead.
Tags:
Source:
Software Foundation
n - 2
A definition of a function that returns n - 2:
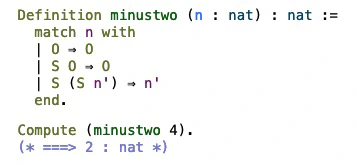
Tags:
Source:
Software Foundation
Fixpoint, Recursion
Recursion is defined using the Fixpoint keyword:

Tags:
Source: